Risk analysis is a crucial component of resource forecasting for datacenters. By identifying and evaluating potential risks, datacenter managers can ensure that their operations are prepared to handle any potential challenges that may arise, allowing them to deliver reliable, high-quality service to their customers. In this blog post, we will explore the different types of risks that can affect resource forecasting in a datacenter. We will also discuss how to use risk analysis to inform resource allocation and capacity planning decisions.
Risk analysis for capacity planning is challenging because there are different sources of variability. Let’s consider 3 major categories of risk for resourcing datacenters:
- Demand variability
- Supply lead time variability
- Repairs and failure variability
Demand Variability represents the fact that customer behavior is unpredictable. Different applications have different levels of variability. E.g., a data warehouse that regularly executes the same set of workflows on a similar-sized dataset for BI would have highly predictable demand. But traffic to Wikipedia probably has a highly unpredictable demand curve that is influenced by real-world events. One way to think about demand variability is to use historical data as a model for demand growth and uncertainty. You could draw a forecast for future demand with different levels of confidence. As you predict further and further out, the error bars add up and you have a wider range of potential demand. This is called the cone of uncertainty. The below figure shows a cone of uncertainty for the minimum demand expected to be presented by customers to the system based on historical variability.
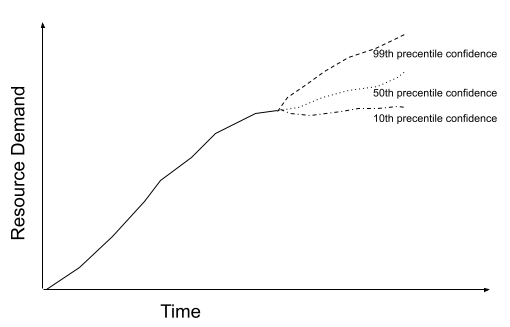
So now we have two questions to answer:
- What confidence level of the cone do we pick for the forecast?
- How far out in time should we forecast?
In a previous blog post, we walked through the process of performance modeling an application (but we cheated on the forecasting problem then). By applying a simplifying assumption that the application will burn its error budget if it does not have all the resources it needs, we could answer the first question by mapping the forecast confidence level to the application SLO. In this case, let’s say we have a P99 SLO, and thus we could choose the forecast line that represents the 99th percentile confidence.
The second question depends on how long it takes us to acquire the resources. In the case of a cloud service, this is simple and often instantaneous or has a small turnaround time for quota increase requests. But if you manage your datacenter, you have to work with your supply chain contract manufacturers to identify the machine lead time. That leads us to the second source of variability.
Supply lead time variability represents the amount of time that the supply chain requires to fulfill an order. This depends on several factors including the length and complexity of the supply chain. The topic of supply chain modeling and optimization is an area of itself that we will cover in a future post. But the key intuition to grasp here is that resource delivery lead times are not deterministic. If you had a supply chain with multiple contracts depending on each other, a delay with a single contractor deep in the chain (say because of procurement delays or unexpected logistics trouble, etc), the delay progresses through the chain in what is called the bullwhip effect.
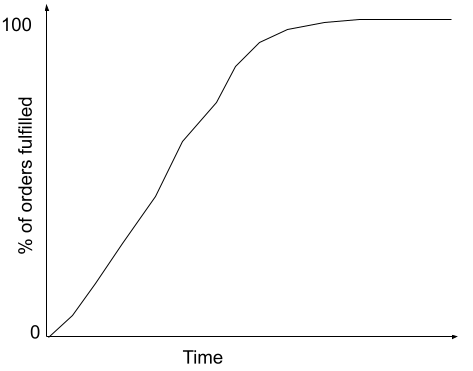
Similar to the demand variability cone of uncertainty, we could draw a similar cone for supply variability as well - either based on historical delivery times or based on the SLAs provided by each of the nodes in the supply chain. A different way to think about this is as a CDF of time to fulfill orders.
Repairs and failure variability finally is the loss of capacity in the datacenter owing to failures and repairs. While supply is the ability to increase resources in the datacenter, this risk loses active resources.
Now that we have stochastic distributions of how these risks are distributed, how can we use this to determine an appropriate level of resource ordering?
Option #1: Choose a confidence interval in the cone of uncertainty based on the application SLO.
The risk offered to the application depends on how correlated the risks are. If they are perfectly correlated to each other, we would expect that the SLO is the MAX(the three confidence percentiles) == MAX(99%, 99%, 99%) == 99% – i.e., we would have a stock out 1% of the time.
But what about the worst-case scenario? If the risks are perfectly anti-correlated, then we would end up using an error budget that is additive i.e., SUM(1% + 1% + 1%) == 3% – i.e., we would stock out for 3% of the time.
In reality, these risks are generally independent of each other, so neither scenario is correct.
Option #2: Use a Monte Carlo simulation to optimize parameter choices.
So the next best option is to simulate the stock-out risk, by sampling from the three distributions. If we rerun the simulation millions of times, this is in effect a Monte Carlo simulation of the system’s resource use. This will allow us to draw a CDF graph of the resource utilization rates. By tweaking the simulation to take different values of confidence percentiles for each of the risk vectors, we could thus also find optimal planning parameters to address each of the risks.
In summary, by drawing deeper insight into the risks involved in resource provisioning, we can mitigate the impact of stock-outs, and ensure the reliability and stability of operations. A key insight here is that these risks can be mitigated by being conservative and holding a large “Safety Stock”. But this buffer of resources comes at a cost. Thus, we are well motivated to keep this inventory as low as possible. Inventory optimization is a large problem in its own right and will be discussed in a subsequent blog post.

